Fraguels, osos amorosos… ¡y agujeros de gusano! ¡Quién lo diría!

Quisiera empezar advirtiendo de un engaño gordo de los muchos que circulan por la red. Hace unos minutos me han enviado un e-mail que dice algo así como que el 27 de agosto se verá en el cielo nocturno a Marte del tamaño de la Luna, y muchos internautas van por ahí haciendo planes de acampada. Antes de buscar el camping gas, estudiemos esto.

Ahora mismo el planeta rojo estará casi 400 veces más lejos de la Tierra que nuestro satélite. Si Marte tiene un diámetro de 6.796 kilómetros y la Luna de 3.476 kilómetros, es irrisorio pensar que Marte se verá del tamaño de la Luna. ¿Cómo lo he deducido? Señores, sé sumar.

Pero no ya será imposible el 27 de agosto, sino cualquier noche del año, del lustro, de la década, del siglo, del milenio o sencillamente cualquier noche habida y por haber. Vamos, que para que Marte se vea tan grandote como la Luna tiene que llegar Dios frotándose las manos diciendo “vamos a ver qué tocamos por aquí”. Pero eso sí (but it so yes), creo que habrá Luna llena justo a la semana siguiente (el 4 de Septiembre), así que esa nochecita sí sería bueno pasear... y cuidadín con los licántropos.

Seguimos. ¿Me habéis dejado una preguntita, verdad? :) El amigo DarkReaper nos planteó si el Gran Colisionador de Hadrones (LHC, para los amigos) “servirá para algo en este campo (en referencia al de los agujeros negros) o está destinado a otras áreas”. La respuesta es que en principio no servirá juasss, pero las conclusiones que se saquen serán luego usadas en las distintas ramas de la Física, incluyendo la de los agujeros negros. Se habla mucho de lo que se logrará con el LHC, pero el 80% es publicidad, así que tras quitar toda la paja nos quedan tres objetivos claramente definidos: averiguar qué es la materia oscura, detectar nuevas dimensiones (si es que las hay) y encontrar el bosón de Higgs. Debajo un bosón, son, son, del señorito Higgs, Higgs, Higgs...

A priori no hará que baje la gasolina, pero saber cuán ciertas son estas tres historias es muy importante. Por una parte, el bosón de Higgs es una partícula elemental que juega un rol fundamental en la Mecánica Cuántica. Se supone que existe, pero por ahora no hay ni rastro del nene. Por otra parte, la materia oscura es casi el 25% de la composición del cosmos, ¡y tampoco sabemos nada de ella! Finalmente, sería interesante calcular de una vez por todas cuántas dimensiones tiene nuestro universo. Recordemos que según mi Teoría de las Fuerzas Excesivas tiene unas 6 ó 7 (ahí estamos, con un par). Esta última línea de investigación sobre las dimensiones, más que para los agujeros negros es de interés para el estudio de los agujeros de gusano, que ahora veremos. Pero antes, quiero decir una cosa:

Jenson Button, líder del campeonato de Fórmula 1, qué crack. Me recuerda a mí.

Eso era lo que quería decir, empiezo con el OcioCiencia ya de veras, que hoy se está haciendo de rogar. En el 1.1 hablamos de cómo actúan los agujeros negros, cosa que no se sabe con seguridad (lo cual honra enormemente nuestro atrevimiento), y dijimos que de ser absorbidos lo mejor era cantar por Carlos Baute, algo que tampoco nadie sabe con seguridad, ni siquiera Carlos Baute. En cierta forma, cantar por estudiar los agujeros negros es como estudiar la muerte: todo el que la experimenta no vuelve para contarlo, y en el tema de singularidades, aunque se habla de que hay un regreso en forma de partículas radioactivas, para el caso es lo mismo... Yo, como co-creador de la rama científica de la Necromática, voy a arrojaros algo de luz acerca de qué se cuece en una singularidad. Ahí va la bombilla, ¡pilladla!

Según afirmó inicialmente Stephen Hawking, dentro de un agujero negro deja de cumplirse el segundo principio de la termodinámica (si no lo recordáis, ahora mismo da igual). Ese principio originaba la flecha termodinámica del tiempo (ver la entrega 0.7) y todo muy bien, pero en resumen: dentro de los agujeros negros el tiempo podría comportarse de otra forma. Al fin y al cabo, los agujeros deforman las dimensiones espaciales, ¿por qué no la dimensión temporal? ¡Uy, lo que ha dicho! ¡Eso daría pie a los agujeros de gusano y a los viajes en el tiempo! ¡Pues claro, amigo, por eso son atajos del espacio-tiempo! ¡A por ellos!

Casi a la vez que los agujeros negros surgió la definición de agujeros de gusano, obra del científico Ludwig Flamm (de huevo). Ya he hablado de esto, pero merece hacerse con más detenimiento. Un flan es un postre que... Digo, la idea que se tiene de un agujero de gusano (su nombre científico es puente de Einstein-Rosen) es la de un hipotético atajo a través del espacio-tiempo, con lo que todo agujero de gusano tendrá al menos dos entradas conectadas por una garganta. Digo “hipotético atajo” porque aún no se ha detectado ninguno. Dibujito al canto:

Ejem, perdonad (cómo estoy hoy). Era este:

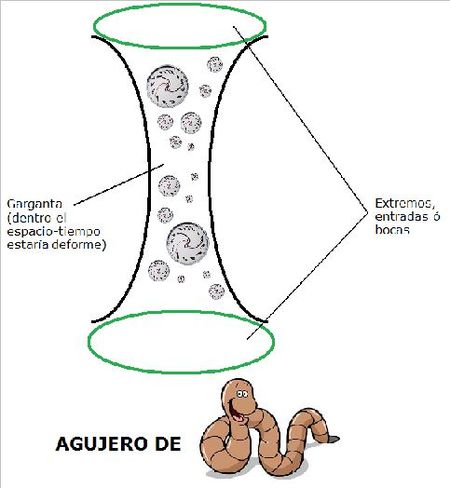
Idea: analogía sencilla para entender los agujeros de gusano. Imaginemos que una madriguera en el suelo tiene dos entradas, dos agujeros. Se podría ir de una entrada a la otra caminado por el suelo (que representa al cosmos), o bien se podría ir a través de la madriguera (que representa al agujero de gusano). Esta última forma nos lleva menos tiempo porque el túnel tendría una longitud más corta que el trozo de suelo a recorrer. Ya tá, se acabó (justo ahora en la calle alguien ha gritado “por fin” xD).

¿Pero por qué sería más corto ir por el agujero de gusano? Primero porque el espacio está curvado. Volviendo a la analogía de la madriguera, esto lo podemos plasmar colocando una montaña entre los dos hoyos. Cualquier viaje por la montaña (o el suelo) nos llevaría más tiempo que a través de la madriguera, que directamente cruza la montaña. La segunda razón, quizás más importante, es que el espacio dentro del agujero de gusano está estirado, con lo que viajar un kilómetro en el agujero podría ser el equivalente a viajar un año-luz en el cosmos. ¡En el futuro no se harán vehículos más rápidos, sino caminos más breves! Y aupa Jenson Button, por supuesto.

Pensemos en un graciosete experimento. Tenemos una regla con dos tornillos, A y B, que están alejados uno de otro 5 centímetros. Supongamos que hay una gomilla de 1 centímetro de longitud sujeta a ambos tornillos (lógicamente deberá estar estirada para cubrir los 5 centímetros). Ahora imaginemos que tenemos un curri (sí, uno de esos obreros renacuajos que salían en Fraggle Rock) sobre la regla y que quiere ir de A a B, pero el pobre sólo puede ir a una velocidad de 1 centímetro por año (un fraguel lento, ciertamente).

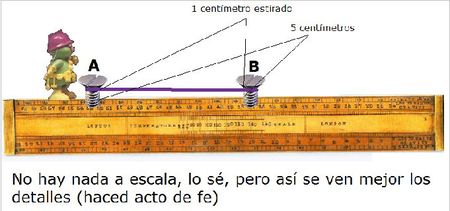
Viajando recto a través de la regla el curri tardaría 5 años (no os riáis, porfa). Sin embargo, si fuese a través de la gomilla, ¡el viaje le tomaría sólo 1 año!, ya que 1 centímetro de espacio en la goma (lo que hay que recorrer) se estira como si fueran 5 centímetros en la regla. Entonces, si el curri coge por el “agujero de gusano” (que aquí es la gomilla), aunque el chaval siga pisando huevos se ahorrará 4 años de viaje.

Todo esto es el modo intuitivo de explicarlo (tengo más analogías que algún día os pondré si tengo ocasión y me sigue faltando vergüenza), porque naturalmente se puede dar con más rigor científico usando ideas topológicas similares a las que nos van a llegar ahora. No asustarse, no muerden. El que quiera obviarlas, puede ir directamente a la sección de más abajo llamada fin del rollo con tecnicismos sin pasar por la casilla de salida y sin cobrar los 6.000. El que sea más valiente (o suicida) que siga leyendo, que le aseguro sangre, sudor y lágrimas, pero pienso que algo aprenderá. O eso, o me le tendrá jurada hasta el fin de sus días, pero el riesgo forma parte de mi vida.

¿Qué es la Topología? ¿Nunca os lo habéis preguntado? ¿A qué se dedican los topólogos? Esas personas tan interesantes que también las quiere Dios, pues también van al Cielo todos los topologuitos buenos. Sabéis de qué hablo. Hablo de esas veces que habéis estado sentados en el banco de un parque y ante vuestras caras pasa un cochazo deportivo, y os quedáis absortos, y al momento os preguntáis ¿qué es eso de la Topología? Bueno, la Topología se conoce como “la Geometría de plastilina” porque en ella los polígonos, rectas, curvas, figuras y demás se pueden encoger, deformar y hacer todo tipo de trastadas siempre que no se “corte” ni se “pegue”. Por ejemplo, redondeando las esquinas de un cuadrado podemos obtener un círculo. Eso topológicamente, sin embargo geométricamente el área de un cuadrado no es la de un círculo. Otro dibujito:

Por este hecho, con mucha maldad se dice que los topólogos no distinguen una taza de una rosquilla (yo he visto que es falso en al menos una ocasión). Vale, de acuerdo, los agujeros de gusano se investigan desde la Topología diciendo que (tomad aire y leedlo cuanto antes) una región compacta del espacio-tiempo tiene un agujero de gusano cuando su frontera es trivial pero su interior no es simplemente conexo. ¡Mi má!, ¿eso qué significa? Por pasos.

Topológicamente, cualquier conjunto tiene frontera e interior. Exclusivamente en lo que veremos a continuación la frontera será el borde y el interior el conjunto sin su borde. Pero cuidado, el que un conjunto topológico los posea no tiene por qué decir que formen parte de él. “Tiene” se refiere a que le corresponde, no a que es suyo. Así, hay conjuntos que sólo son frontera, otros no tienen (en el sentido de que es suyo) frontera pero sí interior, otros tienen interior y frontera (son los llamados compactos) y otros carecen de frontera e interior (son el vacío). Para amenizar la tarde, más dibujitos (los trazos discontínuos indican que no hay frontera):

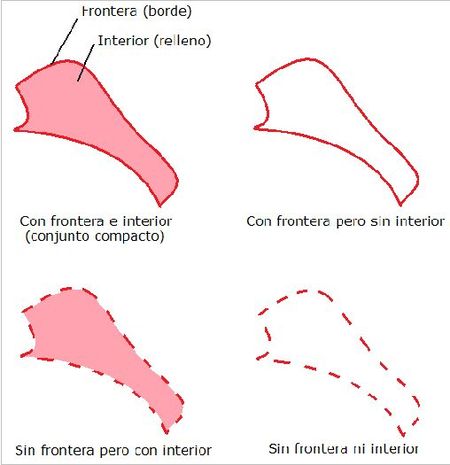
¿Os gusta? A la gente le suele entusiasmar esto, pero es mi deber moral avisaros de que os lo estoy calzando con un tratamiento infantil. Los conjuntos no son siempre figuritas sino cosas más complejas escritas en la antigua lengua de Mordor que no emplearé aquí. Por ejemplo, la frontera a veces no es visible como un borde sino que es más rara que el final de Twin Peaks, y puede consistir en infinitos puntos sueltos, intersección de hiperplanos o vete a saber qué (y mejor no saberlo). Además, hemos dado a entender que todo es negro o blanco, pero no es así de maniqueísta el mundo topológico. No se trata de “tiene” o “no tiene”, a veces un conjunto tiene unos trocitos de frontera, unos trocitos de interior, ¡o sin trocitos en ninguno!, ¡o en los dos por el precio de uno!, y eso complica mucho más las cosas. Aun así, aunque la Topología dé besos amargos, sus labios son dulces. Si alguna vez tengo una hija, llamarla Topología es una opción. “¡Topo, a comer!” no queda tan mal.

Hemos de estar orgullosos de lo aprendido en el párrafo anterior, pero necesitamos saber un poquito (sólo un poquito) más. La Topología también trata las propiedades de estos conjuntos. Una de ellas ya la hemos mencionado: la compacidad. Para entendernos, pensaremos que un conjunto es compacto cuando su frontera y su interior le pertenecen (en el dibujo anterior, en la esquina superior izquierda). Otra propiedad importante es la de conexión. Un conjunto es conexo cuando NO se puede separar en dos conjuntos tal que ninguno está vacío ni tiene puntos en común con el otro. Uf, más fácil pintarlo que decirlo:

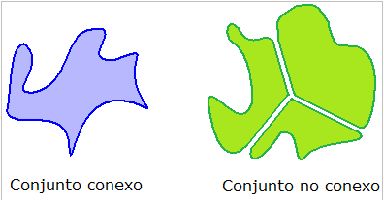
Si un conjunto de dos dimensiones (es decir, en el plano) además de ser conexo no posee “agujeros”, ese conjunto es simplemente conexo.

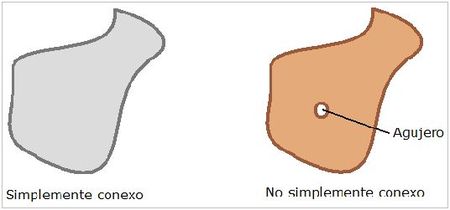
Ya está, no dolió demasiado, lo hicimos con anestesia. Venga, arriba, que éstas son las definiciones más simples que aparecen en el Topología de James R. Munkres, el libro por el que he optado, que es fácil de encontrar, pero leerlo sin conocimientos en Análisis o Espacios Métricos es cosa de kamikazes, sobre todo porque Munkres no tiene mi labia ni mi talento, ejem. Naturalmente, para las deficiones que hemos visto existen más caracterizaciones, más formas de decir lo mismo (un vaso está medio lleno, y a la vez está medio vacío) y, aunque son más complicadas, también son más productivas. De no ser así, los topólogos las manejarían porque son masocas. Yo sé de uno que afirmó tal cosa, pero del resto no tengo ni idea, así que por ahora les daremos el beneficio de la duda.

Todo queda dicho, la suerte está echada. Volvemos al tema de los agujeros de gusano. ¿Preparados para la terapia de choque? A partir de lo dado, la definición rara de antes nos viene a decir que una región del espacio-tiempo (de 3 dimensiones, en nuestro caso) con frontera e interior (compacta) tiene un agujero de gusano cuando carece de frontera (se dice que es trivial) y en su interior existe al menos un agujero (esa región no es simplemente conexa). ¿Ahora mejor? Pues ale, eso era, pero tened en cuenta que el agujero de gusano se define con 4 dimensiones, y no con 3. Eh... si no está más claro, os juro por la narizota de Snoopy que más no lo puedo suavizar sin cometer un sacrilegio cosmológico.

Esto no ha hecho más que empezar. Cuando miramos una manzana siempre vemos un mismo tipo de agujero de gusano, pero cuando se trata de mirar el universo teóricamente existen varios tipos según en qué nos fijemos. Por una parte, si estamos interesados en saber a dónde nos llevará tenemos dos tipos. Si nos lleva a otro lugar de este universo (da igual en que instante temporal) estaremos ante un agujero de gusano de intra-universo. Si en cambio nos lleva a un universo paralelo en el que, por ejemplo, los Jardines Colgantes de Babilonia no fueron destruidos o, lo que es mejor, Rodolfo Chikilicuatre ganó Eurovisión, entonces tenemos un agujero de gusano de tipo inter-universo, también conocido como agujero de gusano de Schwarzschild.

Llegados a este punto os puedo confesar que, como en el cosmos no parecen existir osos de colores, siempre pensé que los Osos Amorosos irrumpían en nuestro planeta usando algo similar. Lo mismo puede aplicarse para la vaca de Milka. La pena es que este último tipo de agujero de gusano, en caso de existir, sería tan inestable que, según probaron Robert Fuller y John Wheeler (este último inventó el término agujero negro), acabaría por desintegrarse casi al momento de formarse, descuartizando salvajemente a cualquier tierno osito que pusiera un pie en él. Después de las clases algunos compañeros nos planteamos esto (un poco en broma). Supusimos que un ser con distinta composición cromática había logrado visitar nuestra realidad. Cada uno de nosotros llegó a interesantes conclusiones como que las longitudes de onda del universo de ese ser debían ser distintas o bien que no era más que un caso particular, al igual que nosotros, dentro de un multiverso. Yo obtuve como solución que en esa visita el color debía jugar un importante papel como dimensión adicional, y así empecé a intuir que nuestro universo debe tener unas 6 ó 7 dimensiones, pero no lo he logrado demostrar. En efecto, ese fue el humillante comienzo (aunque muy, muy primordial) de mi Teoría de las Fuerzas Excesivas (cualquier excusa es buena para promocionarla). Y ahora hacedme el favor de olvidar ese episodio de mi vida, ¿vale? Yo lo hice. Todo el mundo tiene derecho a... Da igual, ¡no pienso dimitir!

Por otra parte, cuando hablamos de los agujeros de gusano, no basta con saber a dónde nos llevarían, también deberíamos pensar si nos llevan en la dirección buena o no. Esto es, al ir por un agujero de gusano podríamos estar yendo contramano como se ven a algunos niñatos en moto por las calles. Bueno, no creo que se diera el caso, el agujero no sería tan permisivo como el asfalto. Al igual que la interacción gravitatoria no nos deja volar, en caso de ir en mala dirección el agujero nos arrojaría fuera con sólo asomar la nariz. Así que otra propiedad de los agujeros de gusano es que son bordes.

En base al criterio de la dirección en que se pueden recorrer los agujeros distinguimos tres tipos. Por una parte está el agujero de gusano infranqueable, que está prácticamente sellado. En sus dos entradas pone “no se admiten visitas”. Por otro lado está el que es franqueable en una dirección. Con éste, como cantara el grupo de metal progresivo Dream Theater en su “Fatal Tragedy”, there can be no turning baaack... Es decir, si te metes no puedes volverte y ya toca salir por la otra abertura. Queda un tercer tipo... Chan, chán (suspense)... El agujero de gusano de Lorentz, accesible en ambas direcciones. Este último es claramente el más interesante, pues nos permitiría ir del pasado al futuro...

Y justo ahora que la cosa se ponía calentita nos paramos. Soy consciente de que os dejo con la miel en los labios, pero así es el marketing. En nuestra próxima entrega, que pondrá cierre a este capítulo, veremos cosas más curiosas y fascinantes que de costumbre. Nos plantearemos con todo rigor científico la posibilidad de viajar en el tiempo y, de ser así, qué nos podría suceder, algo que desembocará en la hipotésis de universos paralelos (para lelos, para mí) y en cosas muy absurdas, cosas que rozan la ciencia-ficción de calidad. Explícitamente me refiero a esas cosas apropiadas para soltar en tu primera cena con los suegros o cuando estés a punto de dar el “sí, quiero” en la Iglesia.

Yo me voy ya en mi coche nuevo, ¡hasta entonces! ¡No me falten!